-El triangulo
1,1 propiedades y tipos de triangulos:
Un lado de un triángulo es menor que la suma de los otros dos y mayor que su diferencia.
La suma de los ángulos interiores de un triángulo es igual a 180°.
El valor de un ángulo exterior de un triángulo es igual a la suma de los dos interiores no adyacentes.
En un triángulo a mayor lado se opone mayor ángulo.
Si un triángulo tiene dos lados iguales, sus ángulos opuestos también son iguales.
1,2 rectas y puntos notables del triangulo.
1,3 el teorema de pitagoras.
El teorema de Pitágoras establece que en todo triangulo rectangulo, el cuadrado de la hipotenusa (el lado de mayor longitud del triángulo rectángulo) es igual a la suma de los cuadrados de los catetos (los dos lados menores del triángulo, los que conforman el ángulo recto).
Si un triángulo rectángulo tiene catetos de longitudes 
y 
, y la medida de la hipotenusa es 
, se establece que: 
.
y , y la medida de la hipotenusa es , se establece que: .1,3.1 demostracion grafica:
1,3.2 el teorema en 3D.
1,4 ¿como calcular la altura de un arbol a partir de su sombra?
Nominamos los vértices con las letras A, B y C.
Tenemos que averiguar cuanto mide el lado AB, que por ahora será igual a X.
Medimos la longitud de la sombra, que es el lado BC. Supongamos que tiene 21.36 metros.
Con ese dato todavía no podemos calcular X.
El paso siguiente es tomar un referente de un metro de altura (A’B’) y medir su sombra (B’C’). Supongamos ahora que la sombra de éste objeto es igual a 1.78 metros. Esto se tiene que hacer enseguida de medir la primera sombra, para que no haya una variación en el ángulo de la luz solar. Lo que hicimos no fue otra cosa que construir un triángulo semejante al primero, pero con la diferencia que sabemos dos datos: las medidas de los catetos.
Por relación de triángulos semejantes sabemos que AB/BC = A’B’/B’C’, y que expresado con valores es: X / 21.36 = 1.00 / 1.78
Entonces despejamos el valor de X, que saldrá de calcular: (21.36 × 1.00) / 1.78
X=12.00 metros.
Así de fácil.
Este cálculo no se modifica si el piso tiene pendiente. Pero si objeto estuviese inclinado, bastará con tener la precaución de ubicar nuestro referente de un metro con la misma posición para que el resultado sea el más aproximado posible.
-lugares geometricos:
2,1 ¿que es un lugar geometrico?
Un lugar geométrico es un conjunto de puntos que satisfacen determinadas condiciones o propiedades geométricas.
2,1 ¿que es la mediatriz y la bisectriz?
la mediatriz de un segmento es la linea recta perpendicular a dicho segmento trazada por su punto medio. Equivalentemente se puede definir como el lugar geometrico — la recta — cuyos puntos son equidistantes a los extremos del segmento. También se le llama simetral.
La bisectriz de un ángulo es la recta que pasa por el vértice del ángulo y lo divide en dos partes iguales. Es el lugar geométrico de los puntos del plano que equidistan (están a la misma distancia) de las semirrectas de un ángulo.
2,3 las conicas.
2,3.1 ¿que es una conica?
Se denomina sección cónica (o simplemente cónica) a todas las curvas resultantes de las diferentes intersecciones entre un cono y un plano; si dicho plano no pasa por el vértice, se obtienen las cónicas propiamente dichas. Se clasifican en cuatro tipos: elipse , parabola, hiperbola y circunferencia.
2,3.2 la circunferencia
La circunferencia es una curva plana y cerrada donde todos sus puntos están a igual distancia del centro.La circunferencia sólo posee longitud. Se distingue del circulo en que éste es el lugar geométrico de los puntos contenidos en una circunferencia determinada; es decir, la circunferencia es el perimetro del círculo cuya superficie contiene.
2,3.3 la elipse.
Una elipse es la curva simétrica cerrada que resulta al cortar la superficie de un cono por un plano oblicuo al eje de simetría –con ángulo mayor que el de la generatriz respecto del eje de revolución.1 Una elipse que gira alrededor de su eje menor genera un esferoide achatado, mientras que una elipse que gira alrededor de su eje principal genera un esferoide alargado.
-obtencion en un cono:
-metodo del jardinero:Primero deben dibujarse perpendicularmente los dos ejes de coordenadas en el suelo y situar el eje Y en la dirección N-S, y el eje X en la dirección E-O.
Luego hemos de señalar los dos focos que están en el eje X a ambos lados del centro a una distancia c (ver como se calcula este valor), es decir, en los puntos (c,0) y (-c, 0).
Despues, con una cuerda que tenga de longitud l = 2a y colocando los extremos en los focos señalados, dibujar la elipse tal como se ve en la figura.
Sólo tendremos que señalar en la elipse los puntos horarios y los puntos que en el eje Y señalarán nuestra posición.
.mesa de billar eliptica: Coloca la bola en el foco “F” e impúlsala con el taco en la dirección que quieras. Siempre entra en el agujero, salvo imperfecciones en la nivelación o excesivo efecto en la bola.
También entrará la bola si la lanzas desde otro sitio pero la haces pasar por el foco “F”.
En una elipse, las líneas que unen los focos con un punto cualquiera de la curva forman con ella (con su tangente) ángulos iguales. Luego si la bola viene por una de esas líneas, después de “reflejarse” en la curva seguirá por la otra línea y, por tanto, pasará por el otro foco. Ahí hemos puesto el agujero.
También entrará la bola si la lanzas desde otro sitio pero la haces pasar por el foco “F”.
En una elipse, las líneas que unen los focos con un punto cualquiera de la curva forman con ella (con su tangente) ángulos iguales. Luego si la bola viene por una de esas líneas, después de “reflejarse” en la curva seguirá por la otra línea y, por tanto, pasará por el otro foco. Ahí hemos puesto el agujero.
2,3.4 la hiperbola:Una hipérbola (del griego ὑπερβολή) es una seccion conica una curva abierta de dos ramas obtenida cortando un cono recto por un plano oblicuo al eje de simetría, y con ángulo menor que el de la generatriz respecto del eje de revolución.
-obtencion en un cono:
-la lampara hiperbolica: Muchos tienen en sus casas esas lámparas con pantalla que se usan en los living-rooms o en la mesas de luz de las habitaciones, que al estar encedidas emanan un cono de luz hacia arriba y otro hacia abajo, los cuales forman sobre la pared dos figuras con forma de hipérbole.
Las figuras sobre la pared, formadas por la luz de la lámpara, se pueden reproducir experimentalmente tomando las medidas de cualquier lámpara del tipo que tengamos en casa y de su posición relativa a la pared. El siguiente gráfico muestra la geometría utilizada para tomar estas medidas:
– Se define como origen al filamento del foco o bombilla de la lámpara. Los ejes 
e 
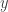forman el plano horizontal con el eje paralelo a la pared y el eje 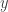perpendicular a la pared. El eje 
es el eje vértical.Para desarrollar una descripción matemática de las figuras proyectadas por la lámpara sobre la pared, utilizando este sistema de coordenadas, es útil considerar a la luz que se sale por los extremos superior e inferior de la lámpara, como los círculos de dos conos simétricos respecto del eje con un origen común situado en el filamento del foco. Los dos conos de luz no son iguales e intersectan la pared en 
. El siguiente diagrama ejemplifica la idea:
e forman el plano horizontal con el eje paralelo a la pared y el eje perpendicular a la pared. El eje es el eje vértical.Para desarrollar una descripción matemática de las figuras proyectadas por la lámpara sobre la pared, utilizando este sistema de coordenadas, es útil considerar a la luz que se sale por los extremos superior e inferior de la lámpara, como los círculos de dos conos simétricos respecto del eje con un origen común situado en el filamento del foco. Los dos conos de luz no son iguales e intersectan la pared en . El siguiente diagrama ejemplifica la idea:
2,3.4 la parabola: En matematicas, una parábola (del griego παραβολή) es la seccion conica resultante de cortar un cono recto con un plano cuyo ángulo de inclinación respecto al eje de revolución del cono sea igual al presentado por su generatriz. El plano resultará por lo tanto paralelo a dicha recta.
-obtencion en un cono:
La trayectoria de una pelota que rebota es una sucesión de parábolas
-la antena parabolica: La antena parabólica es un tipo de antena que se caracteriza por llevar un reflector parabolico, cuya superficie es en realidad un paraboloide de revolución. Las antenas parabólicas pueden ser transmisoras, receptoras o full dúplex, llamadas así cuando pueden trasmitir y recibir simultáneamente. Suelen ser utilizadas a frecuencias altas y tienen una ganancia elevada.
En las antenas parabólicas transmisoras, la así llamada parábolarefleja las ondas electromagnéticas generadas por un dispositivo radiante que se encuentra ubicado en el foco del paraboloide. Los frentes de onda inicialmente esféricos que emite ese dispositivo se convierten en frentes de onda planos al reflejarse en dicha superficie, produciendo ondas más coherentes que otro tipo de antenas.
-el horno solar: Un horno solar es una estructura que usa energía solar concentrada para producir altas temperaturas, usualmente para usos industriales.Reflectores parabólicos o heliostatos concentran la luz de insolacion sobre un punto focal. La temperatura en el punto focal puede alcanzar los 3.500 °C, y este calor puede ser usado para generar electricidad, fundir acero, fabricar combustible de hidrogeno nanomateriales.
-el espejo parabolico: un espejo parabolico es aquel que tiene una forma de antena parabolica, o cuyo perfil es simil con una parabola(y=x²), en el caso de un espejo concavo parabolico (un espejo parabolico convexo es algo bastante inutil, no importa mucho porque...) se aplican las mismas propiedades opticas que en cualquier espejo concavo, si el haz de luz incide paralelamente al eje, el haz de luz refractado pasa por el foco, y por descarte, si el haz de luz incidente pasa por el foco se refleja paralelamente.
Ejercicios de vectores y translación
3.2.1 Dados los vectores u=(4,3) y v=(-1,4), hallar:
a) su representación gráfica en un sistema de coordenadas
b) los vectores u + v y u - v por la regla del paralelogramo
3.2.2 Dibuja las figuras trasladadas de las siguientes en una traslación de vector guía u(4,3):
Resumen de áreas y volúmenes conocidas
Áreas
un cuadrado = a2 
un rectángulo = ab 
un paralelogramo = bh 
un trapesoide = (h/2) (b1 + b2) 
un círculo = pi r2 
un elipse = pi r1 r2 
un triángulo = (1/2) b h 
Volúmenes
un cubo = a3 
un prisma rectangular = a b c 
un prisma irregular = b h 
un cilindro = b h = pi r2 h 
una pirámide = (1/3) b h 
un cono = (1/3) b h = (1/3) pi r2 h 
una esfera = (4/3) pi r3
un elipsoide = (4/3) pi r1 r2 r3 
La esfera y el globo terráqueo
elementos pricipales de la esfera
Centro: Punto interior que equidista de cualquier punto de la esfera.
Radio: Distancia del centro a un punto de la esfera.
Cuerda: Segmento que une dos puntos de la superficie.
Diámetro: Cuerda que pasa por el centro.
Polos: Son los puntos del eje de giro que quedan sobre la superficie esférica.
elementos de la esfera terrestre
he encontrado un video en el que explica claramente y resumidamente los elementos de la esfera terrestre
5.3 Los husos horarios, la hora local solar y oficial.
1. La tierra esta dividida en 24 sectores de 15 grados de longitud
2. entre cada grado de longitud existen 4 minutos de diferencia
3. Cada país debe sincronizar su hora oficial con la solar de manera que corresponda a su posición, de manera que las 12:00pm oficiales se aproximen todo lo posible al mediodía local
5.4 El metodo de erastostenes para calcular la esfera terrestre.
En el solsticio de verano los rayos solares inciden perpendicularmente sobre el Trópico de Cáncer, donde se encuentra Siena (Asuán). En Alejandría, más al norte, Eratóstenes midió la altura de una varilla y la longitud de su sombra proyectada, con lo cual se puede determinar el ángulo formado con el plano de la eclíptica, en el que se encuentran el Sol y la ciudad de Siena; este ángulo es precisamente la diferencia de latitud entre ambas ciudades. Conocida ésta se mide el arco de circunferencia (aproximadamente 7,2º) y se extrapola el resultado a la circunferencia completa (360º).
Sabiendo que entre Siena y Alejandría había unos 500 estadios y que ambas están aproximadamente en el mismo meridiano, el resultado daba una medida para la circunferencia terrestre de 39.614,4 km, frente a los 40.008 km considerados en la actualidad, esto es, un error de menos del 1%.
En el solsticio de verano los rayos solares inciden perpendicularmente sobre el Trópico de Cáncer, donde se encuentra Siena (Asuán). En Alejandría, más al norte, Eratóstenes midió la altura de una varilla y la longitud de su sombra proyectada, con lo cual se puede determinar el ángulo formado con el plano de la eclíptica, en el que se encuentran el Sol y la ciudad de Siena; este ángulo es precisamente la diferencia de latitud entre ambas ciudades. Conocida ésta se mide el arco de circunferencia (aproximadamente 7,2º) y se extrapola el resultado a la circunferencia completa (360º).
Sabiendo que entre Siena y Alejandría había unos 500 estadios y que ambas están aproximadamente en el mismo meridiano, el resultado daba una medida para la circunferencia terrestre de 39.614,4 km, frente a los 40.008 km considerados en la actualidad, esto es, un error de menos del 1%.
En el solsticio de verano los rayos solares inciden perpendicularmente sobre el Trópico de Cáncer, donde se encuentra Siena (Asuán). En Alejandría, más al norte, Eratóstenes midió la altura de una varilla y la longitud de su sombra proyectada, con lo cual se puede determinar el ángulo formado con el plano de la eclíptica, en el que se encuentran el Sol y la ciudad de Siena; este ángulo es precisamente la diferencia de latitud entre ambas ciudades. Conocida ésta se mide el arco de circunferencia (aproximadamente 7,2º) y se extrapola el resultado a la circunferencia completa (360º).
Sabiendo que entre Siena y Alejandría había unos 500 estadios y que ambas están aproximadamente en el mismo meridiano, el resultado daba una medida para la circunferencia terrestre de 39.614,4 km, frente a los 40.008 km considerados en la actualidad, esto es, un error de menos del 1%.
No hay comentarios:
Publicar un comentario